[Bianca]

Ich möchte einen Quilt nähen aus lauter Dreiecken (Half Square Triangles). Die aber in verschiedenen Größen, wobei der quadratische Block aber immer die selbe Größe haben soll:



Ich nähe mit einem Patchworkfüßchen, meine Nahtzugabe ist also immer 1/4 inch. Und wie groß muss ich dann die Dreiecke bzw. die Quadrate vor dem durchschneiden machen?

Das ist jetzt ganz einfach, denn rechnen muss nicht mehr sein! Ich möchte euch diese Lineale vorstellen:



Ich entscheide mich für eine Blockgröße (genähtes Endmaß), das kann auch in cm sein, das spielt keine Rolle. Als Beispiel nehme ich hier 9x9 cm und lege mein Lineal für dieses Endmaß an:



Ich schneide hier nur ein Quadrat, man kann natürlich genau so auch erst Streifen schneiden und die dann zu Quadraten.

Je nachdem wie das Endergebnis aussehen soll, nehme ich eines dieser Linealerweiterungen und lege sie zusätzlich an mein Lineal an. Dann wird an der Außenkante geschnitten



In diesem Fall habe ich die Erweiterung für ein HST gewählt. Ich könnte nun das Quadrat diagonal teilen und die Dreiecke neu zusammen nähen, oder man kann natürlich auch die erst-nähen-dann-schneiden Methode wählen:



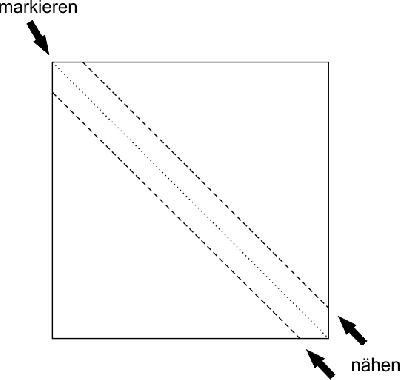
Egal wie man es macht: Solange man bei einer Nahtzugabe von 1/4 inch (oder 6mm) bleibt, kommt am Ende immer das passende Quadrat heraus


_________________
Viele Grüße
Bianca


Patchwork-Schablonen, Lineale, Quilt-Ruler in meinem Shop

[Werbung]

[Medi64]

Du hast mich neugierig gemacht.


LG Medi
_________________
Keine Seifenblase kann so hoch steigen, wie die Phantasie.

[Quiltfrau]

Wenn ich das richtig verstehe, dann kann Dein Zusatzlineal an jedes andere gelegt werden und hat die erforderliche Größe für die zusätzlich erforderlichen Nahtzugaben, je nachdem wie oft ich mein Quadrat noch zerschneiden will.
Gute Idee, spart die Rechnerei.
_________________
Herzliche Grüße Brigitte

"Habe keine Angst etwas Neues anzufangen! Denke immer daran:
Amateure haben die Arche gebaut und Profis die Titanic! "
by Julia "single in der Großstadt"

[Bastelhexe]

Keine schlechte Idee. Ich hab es mir bis jetzt immer einmal vorgezeichnet, auseinandergeschnitten, die Diagonalen plus der Nahtzugabe auf ein neues Papier gezeichnet und die Felder wieder aufgeklebt. Hat bis jetzt auch immer gute Ergebnisse gebracht.
Mit Linealen ginge das natürlich noch einfacher.
_________________
Liebe Grüße
Barbara

"Lernen ist wie rudern gegen den Strom - wer aufhört, treibt zurück."

Mein Blog

[lindaflix]

Wo gibt's diese Lineale denn zu kaufen?
_________________
Gruß aus Bayern von

lindaflix

[Bianca]

[ClaudiaN]

Das ist ja mal eine Klasse Idee. Ich habe mich bis jetzt immer halb totgerechnet.
_________________
Liebe Grüße aus dem Erzgebirge

Claudia

Jetzt auch mit Blog http://stoffpaula.blogspot.de/

[Medi64]

Mein Päckchen ist schon unterwegs

Danke Bianca

LG Medi
_________________
Keine Seifenblase kann so hoch steigen, wie die Phantasie.